はじめに
本記事では,ABテスト (並行テスト) のデータに対してt検定を行うことの問題点について説明します。
以下では,これらの問題についてRコードも交えながら説明していきます。
モデル
ABテストや並行テストといっていますが,モデルとしては基本的な時系列モデルです。
\( \displaystyle
y_{0, t} = \mu + \beta_0 * t + \phi * y_{0, t-1} + \epsilon_{0, t} \\
y_{1, t} = \mu + \beta_0 * t + \phi * y_{1, t-1} + \beta_1 * t + \gamma + \epsilon_{1, t} \\
\epsilon \sim N(0, \sigma^2)
\mu: 水準 \\
\beta_0: 傾き (トレンド) \\
t: 時点 \\
\phi: 自己相関の程度 \\
\beta_1: バージョンBの傾き
\gamma: 水準の変化 \\
\sigma: データのsd
\)
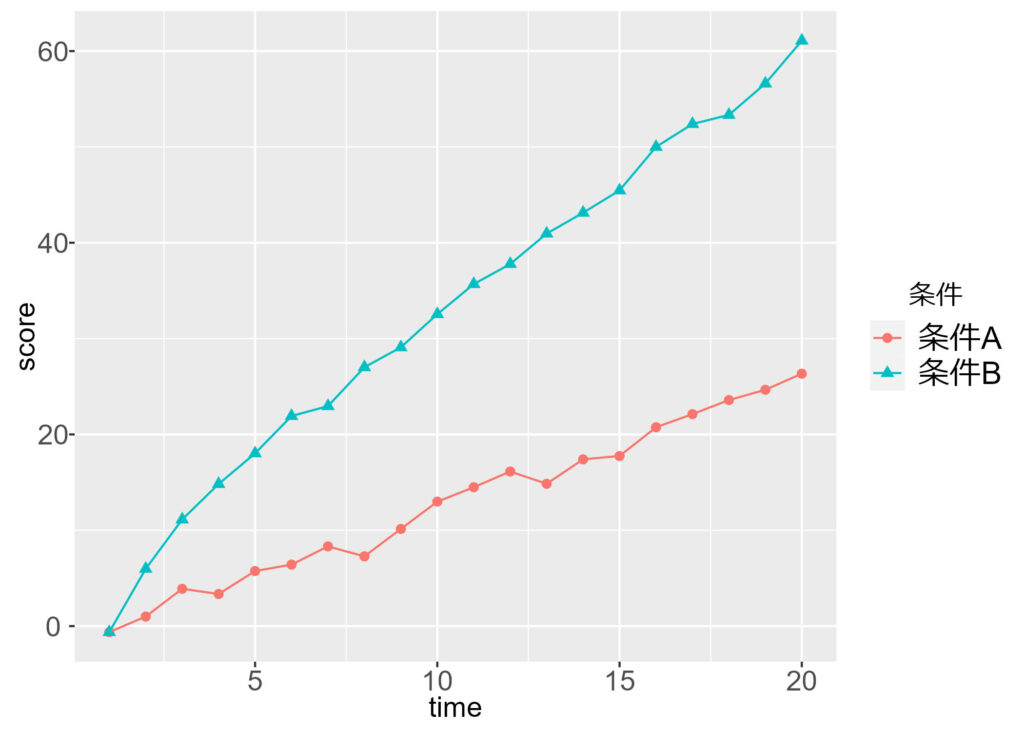
例えば,下図は \( \mu = 0, \beta_0=1, \beta_1=1, \gamma=5, \phi=0.3, \sigma=1 \) の場合のデータ例です。傾きがバージョンB (条件B) で大きいので,バージョンBの効果があると言えます。
データ生成とシミュレーションのRコード
データ生成用の関数は以下になります。まずは初期値y[1]を作っておいて,後は時系列データなので,再帰的に従属変数yを作成していきます。上記のモデルをコードに移しただけです。
#- データ生成用関数
data_gen <- function(mu, beta0, beta1, gamma, phi, sigma, N) {
y0 <- y1 <- numeric(length = N) # 従属変数
y0[1] <- y1[1] <- mu + rnorm(n = 1, mean = 0, sd = sigma) # 初期値 (群間差はなし)
# データの生成
for(t in 2:N) {
error <- rnorm(n = 2, mean = 0,sd = sigma)
y0[t] <- mu + beta0 * (t-1) + phi * y0[t-1] + error[1] # 統制群
y1[t] <- mu + beta0 * (t-1) + phi * y1[t-1] + beta1 * (t-1) + gamma + error[2] # 実験群
}
data <- as.data.frame(cbind(1:N, y0, y1))
return(data)
}
これをもとにして,データ生成→検定を繰り返すシミュレーション実験を実行する関数が以下になります。
なお,条件B (バージョンB, 実験群) の方が値が上昇することが良いことと定義し,t検定では片側検定を実施しています。
#- シミュレーション繰り返し用関数
cond_sim <- function(mu, beta0, beta1, gamma, phi, sigma, N, Iter=10000) {
#- データ生成と検定
res_test <- numeric(length = Iter) # 検定結果の格納
for(iter in 1:Iter) {
temp_y <- data_gen(mu = mu,beta0 = beta0,beta1 = beta1,gamma = gamma,phi = phi,sigma = sigma,N = N) # データ生成
res <- t.test(temp_y$y0, temp_y$y1) # t検定
if((res$p.value < 0.05) & (diff(res$estimate) > 0)) { # 差の符号も気にするように (phase Bが上がる想定)
res_test[iter] <- 1 # 有意
}else {
res_test[iter] <- 0 # 有意差なし
}
} # for loop
# 有意になった割合を返す
return(mean(res_test))
}
t検定を行うと問題が生じることの確認
自己相関 (の絶対値) が大きくなると検出力が下がる
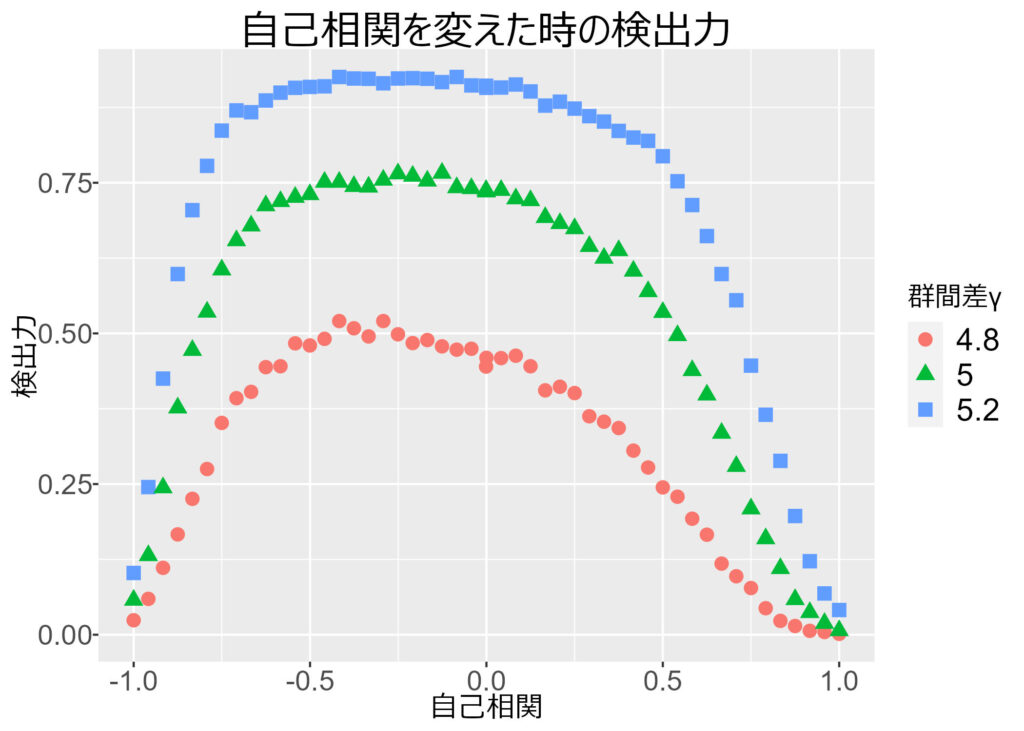
以下の図を見てください。
この図では,自己相関 (x軸) を動かしたときの,検出力 (y軸) を確認しています。また,群間の水準差を表すγは,3条件用意しています。
この図から分かるように,群間差がある (効果がある) 時に,きちんと効果があると言える確率 (検出力) は,自己相関が0の付近で大きくなります。端にいくほど検出力は下がってしまいます。
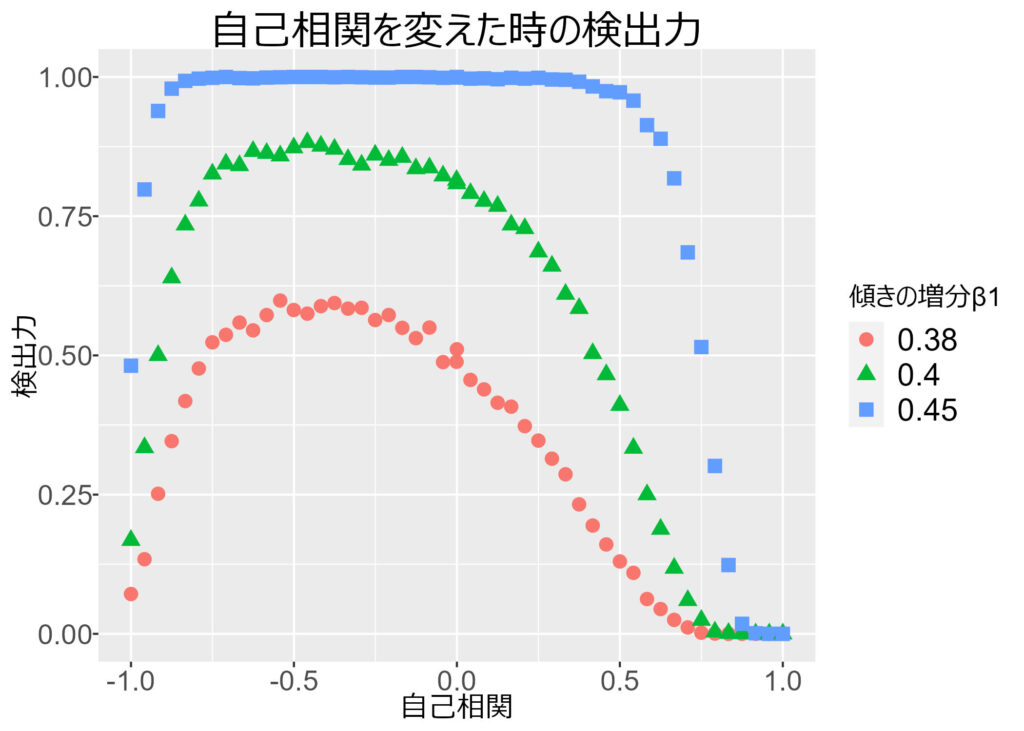
この傾向は,バージョンBにおける傾きβ1を動かしても同様です (下図)。
シミュレーションコード
γを変化させる場合のコードは以下のようになります。
mu <- 0 # ベースの水準
gamma_seq <- c(4.8, 5, 5.2) # 群間差γ
seqN_phi <- 50 # 自己相関の条件数
phi_seq <- c(seq(-1, -0.001, length.out=seqN_phi/2), seq(0, 1, length.out=seqN_phi/2)) # 自己相関の条件
res_plot <- matrix(NA, nrow = seqN_phi, ncol = length(gamma_seq)) # 格納用
for(i in 1:seqN_phi) {
for(j in 1:length(gamma_seq)) {
res_plot[i, j] <- cond_sim(mu = mu,beta0 = 1,beta1 = 0,gamma = gamma_seq[j],
phi = phi_seq[i],sigma = 1,N = 30,Iter = 2000)
}
print(i)
}
β1を変化させるコードは以下になります。
mu <- 0 # ベースの水準
beta1_seq <- c(0.38, 0.4, 0.45) # trend差β1の条件
seqN_phi <- 50 # 自己相関の条件数
phi_seq <- c(seq(-1, -0.001, length.out=seqN_phi/2), seq(0, 1, length.out=seqN_phi/2)) # 自己相関の条件
res_plot <- matrix(NA, nrow = seqN_phi, ncol = length(beta1_seq)) # 格納用
for(i in 1:seqN_phi) {
for(j in 1:length(beta1_seq)) {
res_plot[i, j] <- cond_sim(mu = mu,beta0 = 1,beta1 = beta1_seq[j],gamma = 0,
phi = phi_seq[i],sigma = 1,N = 30,Iter = 2000)
}
print(i)
}
データ数が増えても検出力が上がらないことがある
通常,データ数 (サンプルサイズ) が多くなると,検出力は上昇します。
しかし,並行テストにおけるt検定の場合は,不思議なことにこの傾向がみられないことがあるようです。
具体的には,β1が0ではない (効果がある) 場合はデータ数と検出力は比例関係があります。一方で,γが0でない (効果がある) 場合は,データ数が増えるとむしろ検出力は下がります。
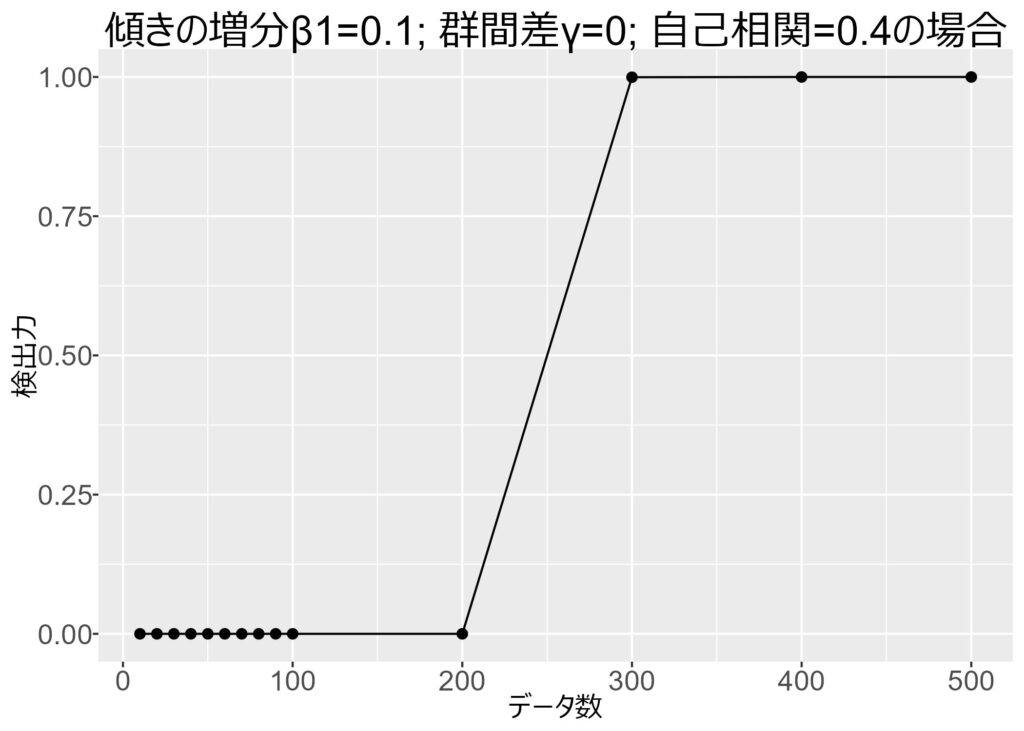
以下の図は,データ数 (x軸) を動かした時の検出力です。条件Bの傾きの増分は0.1です。つまり,条件Aより条件Bの方が傾きが0.1大きい状態です。γは0という設定です。
データ数が200を超えたところで,ようやく意味のある差を検出できるようになります。
一方で,以下の図は,β1は0で,γが8という設定です。γが0ではないため,この設定も条件Bの効果があると言えます。
データ数が100を超えたところで,検出力が一気に低くなっています。
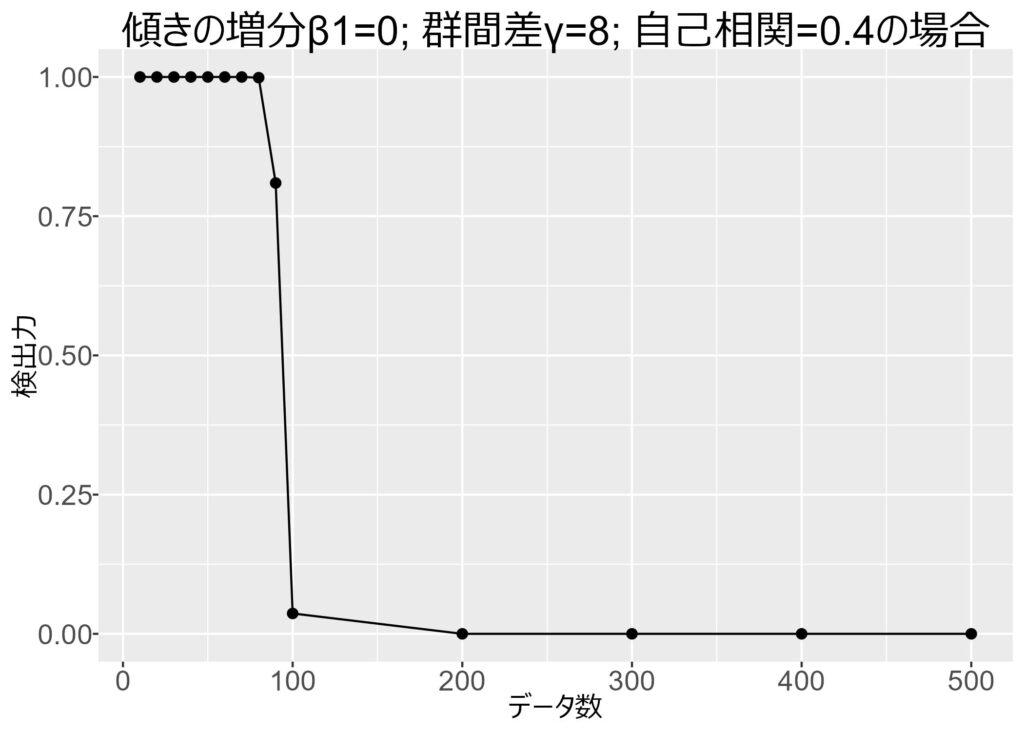
普通は,サンプルサイズが多いほど,検出力は大きくなるべきです。
この挙動は異常な性質であり,並行テストに対して,t検定を適用した場合は,おかしなことが生じえます。
まとめ
以上のシミュレーションで示してきたように,単純なt検定やカイ二乗検定をABテスト (並行テスト) に適用すると,検出力が低くなってしまいます。
そのため,しっかりと時系列モデリングを行い,条件A, Bの傾きや水準,自己相関を推定したうえで,効果の大きさを測っていく必要があります。
ニーズと機会があれば,ABテスト (並行テスト) におけるモデリングの話題も執筆しようと思います。質問等があれば,コメントお待ちしております。


コメント