ABテストの分析法について
前編では,ABテストには大きく分けて並行テストと逐次テストがあることを説明しました。
また,いずれにおいても,t検定やカイ二乗検定が利用されることが多いことを説明しました。
しかし,このt検定 (やカイ二乗検定) を利用することには問題があります。
この理由を説明する前に,水準と傾きについて復習しておきます。
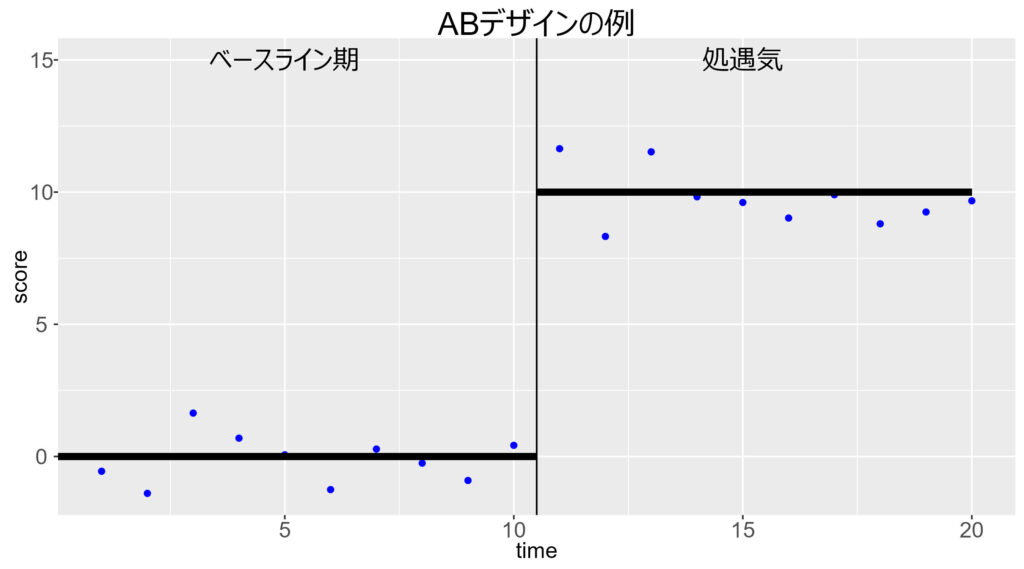
左図は,逐次テストにおいて,バージョンA (ベースライン期) とバージョンB (処遇期) で,水準が異なる例です。
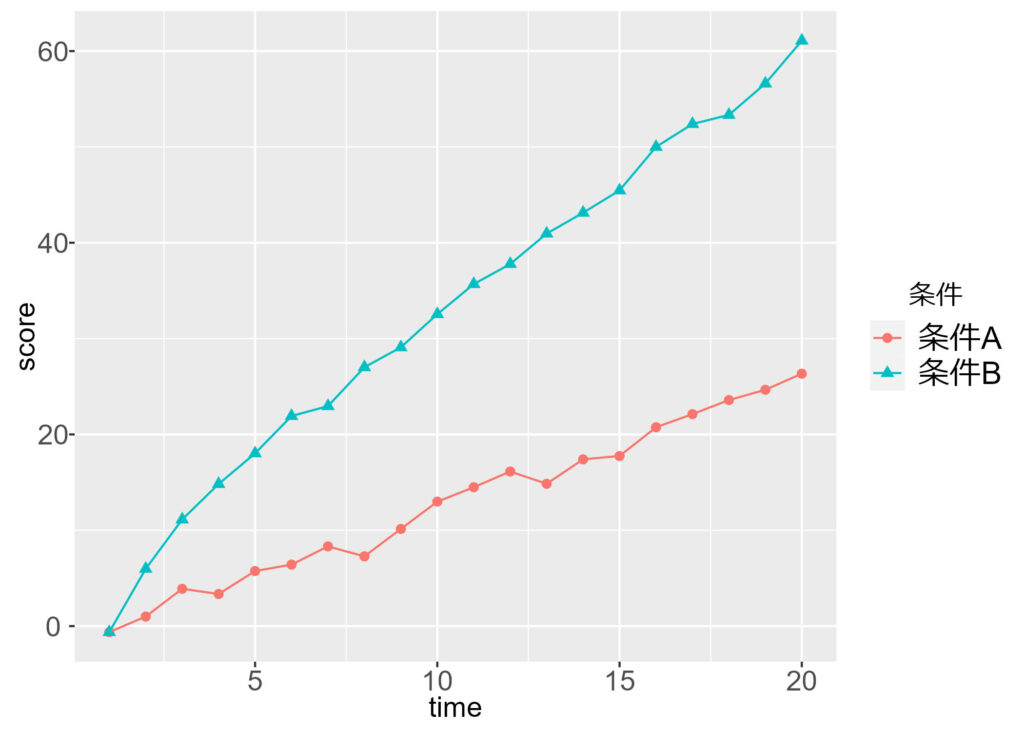
右図は,バージョンA, B間で傾きが異なる例です。
いずれにおいても,平均値の差は生じています。そのため,t検定などを行うと,有意差が見いだされるはずです。
しかし,t検定などを実施すると,水準や傾きに違いがないのに,単純な平均値差が生じてしまうことがあります。そのため,t検定などを使用するのは望ましくない場合があります。以下では,逐次テストと並行テストに分けて,説明します。
並行テストでt検定やカイ二乗検定を使用すべきでない理由
1. 自己相関が大きい場合,検出力が低下する
t検定では,データが独立に出てきていることを仮定します。
独立とは,1個目のデータと2個目のデータが関係ないということです。1個目のデータから2個目のデータの大小を予測できないと言うこともできます。
一方で,定期的にクリック率やPV数を取得するような,いわゆる時系列データの場合,直前のデータの影響を受けることがあります。このような場合,1個目のデータと2個目のデータが関連する (相関がある) のです。これを自己相関と言います。
つまり,厳密にはt検定を適用するために必要な条件が満たされていません。
実際にシミュレーションを行うと,自己相関 (の絶対値) が大きいほど,検出力が下がってしまうことが分かりました。つまり,本当は広告の効果があるので,効果がないという判断を誤ってしやすくなります。
2. データ数を増やしても検出力が上がらないことがある
基本的に,サンプルサイズを増やすと,検出力は大きくなります。
なお,サンプルサイズとは要するに取得するデータ数のことだと思ってもらって大丈夫です。
しかし,奇妙なことに,並行テストに対してt検定を実行すると,サンプルサイズを増やしても検出力が上昇しないことがあります。
これもシミュレーション実験を行うことで確かめることができます。
逐次テストでt検定を使用してはいけない理由
逐次テストで,単純に平均値差を調べるt検定を使用していけない理由は,直感的に分かりやすいと思います。以下では,図を交えて説明します。
1. トレンド (傾き) がある場合,Type I error率が上がる
以下の図を見てください。
例えば,売上やPV数は右肩上がりに増えていっている (トレンドがある) 状況を考えましょう。図の縦線 (time = 11あたり) で,バージョンBに切り替えたとします。
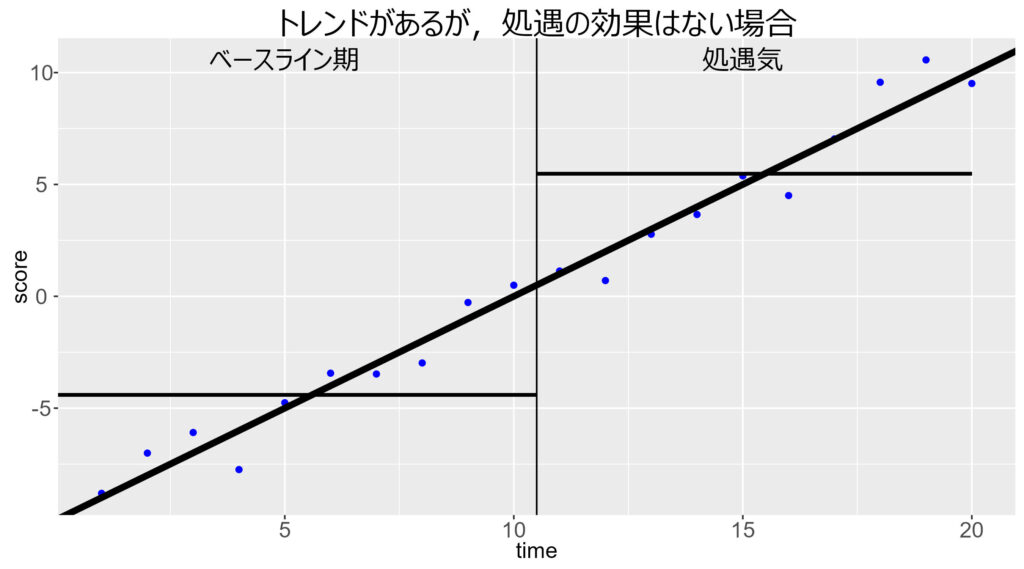
横線は,各フェーズでの平均値を表す。
この例では,上昇トレンドも変化していなければ,水準も (ジャンプして) 変化していません。つまり,バージョンB (あるいは広告) の効果はありません。
しかし,元々上昇トレンドがあるために,単純な平均値には差が生じてしまいます。
つまり,バージョンBには「効果がない」というのが正しいのに,t検定の結果は「効果がある」と判断してしまいやすくなります。このようにType I error率が上がるのです。
2. 自己相関がある場合にType I error率が上がる
自己相関がある場合に,どのような不都合が生じるかは分かりづらいのですが,図を使って説明します。
以下は,自己相関が正の場合の図です。
自己相関が正のため,値が正になったら正の範囲にとどまりやすく,値が負になったら負の範囲に留まりやすくなります。
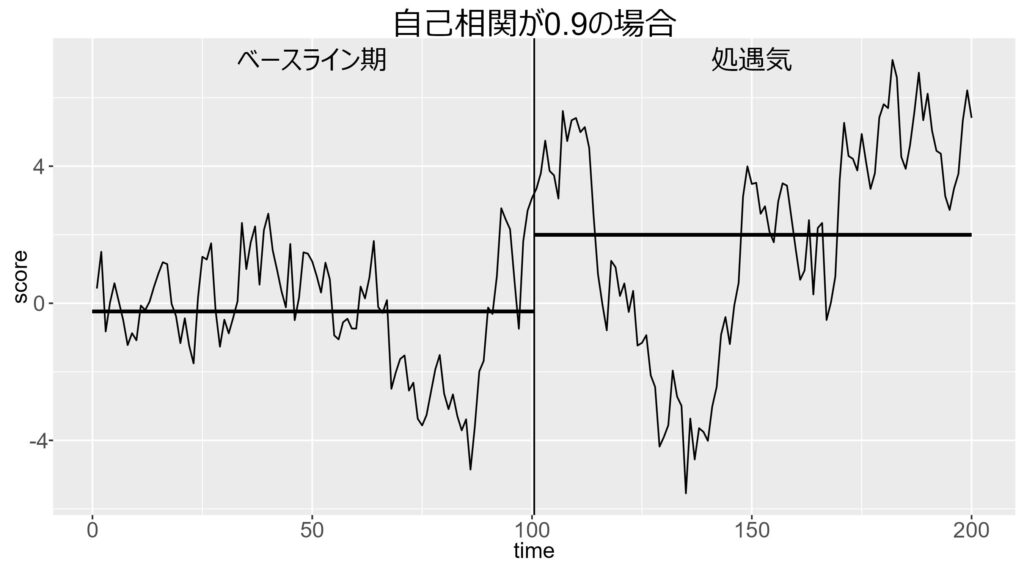
一方で下図は,自己相関が負の場合です。
値が大きくなると,次の値は小さくなりやすくなるので,よりギザギザした線になることが分かります。
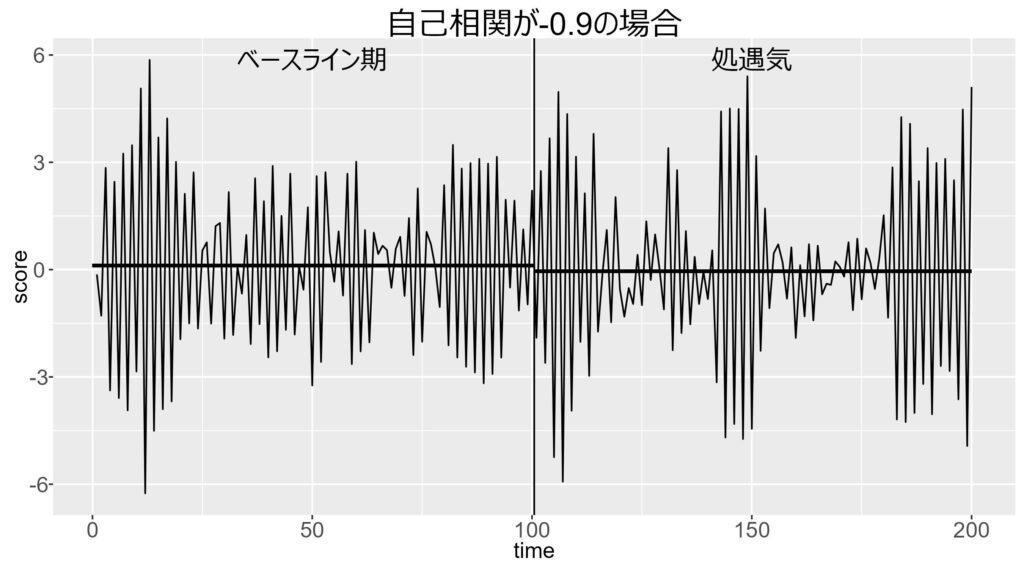
以上の図から,自己相関が正の場合は,あまりジグザグとはしないため,平均値差が見いだされやすいことが分かります。実際に,自己相関が正の場合は,Type I error率が高まります。
一方で,自己相関が負の場合は,平均値差が見いだされにくく検出力が下がります。
3. 傾きが逆方向に変化した場合,検出力が下がる
例えば,一日のPV数が減少傾向にある (傾きが負) としましょう。その状況に対して,とある施策をしたところ,PV数が増加傾向に転じた (傾きが正) とします。
これは明らかに,施策 (バージョンB)の効果はあります。しかし,以下の図のように,単純な平均値には差が生じません (バージョンA, Bの期間=データ数が同一の場合)。
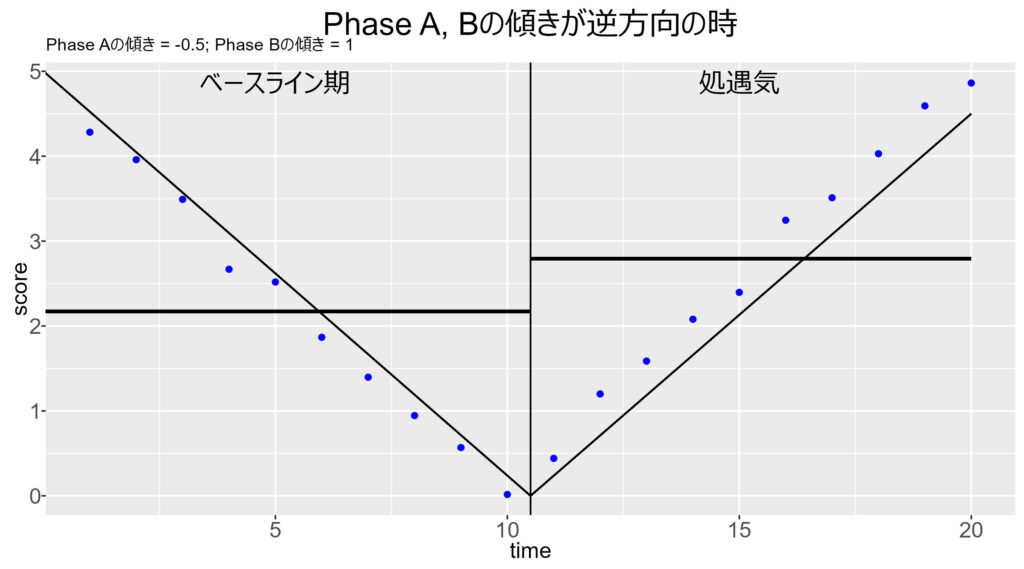
上記の場合は,実際にt検定を行うと,有意差は認められません。
単純なt検定やカイ二乗検定では限界があるのです。
ABテストにおける分析法
t検定などは,自己相関を考えていないことや,平均値差だけを見ており傾きなどは考えていないことを説明しました。
この問題を解決するためには,自己相関や傾きを取り入れたモデルをベースにして仮説検定を行えば良いです。
例えば,傾きや自己相関を取り入れた時系列モデルを適用するということが考えられます。
機会やニーズがあれば,ABテストにおける時系列モデルなどについても説明しようと思います。
ABテストの分析法に関して専門家ではない場合は,計画・分析の案件も受けておりますので,お問い合わせください。


コメント