ABテスト (逐次テスト) においてt検定は使ってはいけない

はじめに

本記事では，逐次テストのデータに対してt検定を行うことの問題点について説明します。

以下では，これらの問題についてRコードも交えながら説明していきます。

モデル

本記事では，傾きや自己相関を考えた以下のモデルによってシミュレーションデータを生成します。

\( \displaystyle
y_t = \mu + \beta_0 (t – n_0) + \phi y_{t-1} + \beta_1 (t – n_0) X_t + \gamma X_t + \epsilon_t, \\
\epsilon_t \sim Normal(0, \sigma^2), \\
\mu: フェーズAの水準 \\
\beta_0: フェーズAの傾き (トレンド) \\
t: 時点; n_0: フェーズAのデータ数 \\
\phi: 自己相関の程度 \\
\beta_1: フェーズBの傾きの変化量
X_t: フェーズを表す変数, 0ならフェーズA，1ならフェーズB \\
\gamma: 水準の変化 \\
\sigma: データのsd
\)

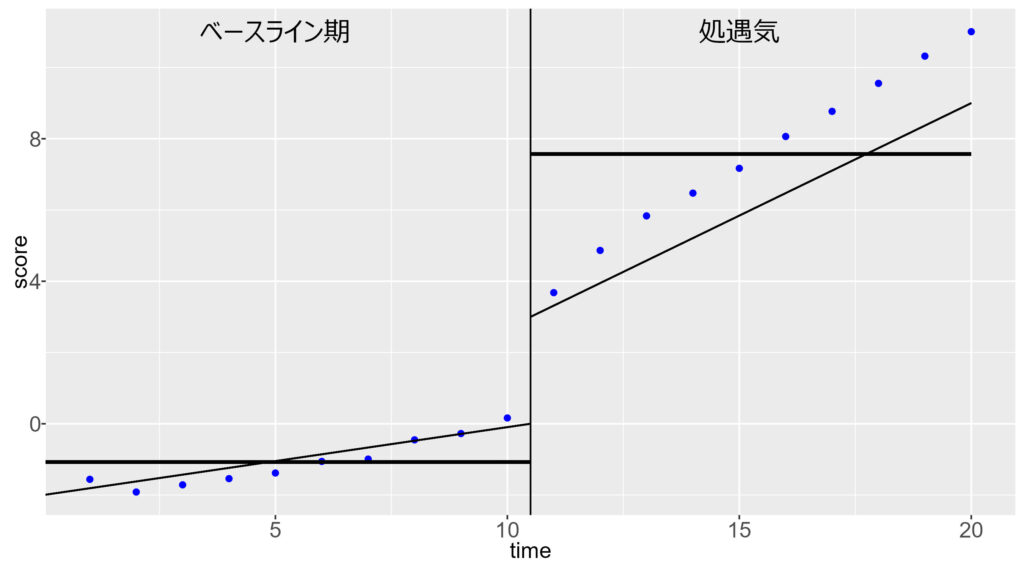
例えば，下図は \( \mu = 0, \beta_0=0.2, \beta_1=0.4, \gamma=3, \phi=0.2, \sigma=1 \) の場合のデータ例です。傾きが処遇期で急になり，水準も処遇期でジャンプして変化しており，バージョンB (処遇，操作) の効果があることが分かります。

データ生成とシミュレーションのRコード

データ生成用の関数は以下になります。まずは初期値y[1]を作っておいて，後は時系列データなので，再帰的に従属変数yを作成していきます。上記のモデルをコードに移しただけです。

#- データ生成用関数
data_gen <- function(mu, beta0, beta1, gamma, phi, sigma, X) {
  n0 <- length(which(X == 0)); n1 <- length(which(X == 1)) # データ数
  y <- numeric(length = n0+n1) # 従属変数の箱
  y[1] <- mu + beta0*(1-n0) + rnorm(n = 1, mean = 0, sd = sigma) # 初期値を作成
  # データの生成; t = -n0+1, -n0+2, ...,-1, 0 (phase Aの最後), 1 (phase Bの最初), ..., n1-1, n1
  for(t in 2:(n0+n1)) {
    y[t] <- mu + beta0*(t-n0) + beta1*(t-n0)*X[t] + gamma*X[t] + phi*y[t-1] +
      rnorm(n = 1,mean = 0, sd = sigma) # 再帰的計算
  }
  return(y)
}

これをもとにして，データ生成→検定を繰り返すシミュレーション実験を実行する関数が以下になります。
なお，Phase Bの方が値が上昇することが良いことと定義し，t検定では片側検定を実施しています。

#- シミュレーション繰り返し用関数
cond_sim <- function(mu, beta0, beta1, gamma, phi, sigma, n0, n1, Iter=10000) {
  #- phase A, Bを表す説明変数
  X <- c(rep(0, n0), rep(1, n1))
  #- データ生成と検定
  res_test <- numeric(length = Iter) # 検定結果の格納
  for(iter in 1:Iter) {
    temp_y <- data_gen(mu = mu,beta0 = beta0,beta1 = beta1,gamma = gamma,phi = phi,sigma = sigma,X = X) # データ生成
    res <- t.test(temp_y[1:n0], temp_y[(n0+1):(n0+n1)]) # t検定
    if((res$p.value < 0.05) & (diff(res$estimate) > 0)) { # 差の符号も気にするように (phase Bが上がる想定)
      res_test[iter] <- 1 # 有意
    }else {
      res_test[iter] <- 0 # 有意差なし
    }
  }
  
  # 有意になった割合を返す
  return(mean(res_test))
}

t検定を行うと問題が生じることの確認

Phase A (β0) に傾きがあると，Type I error率が上昇する

WebサイトのレイアウトをバージョンAからバージョンBに変更したときに，バージョンBの方がコンバージョン率が高まるかを知りたいとしましょう。ただし，Phase Aに既に傾きがあるとします。
成長中の企業ならコンバージョン率自体も微増傾向になることはあり得ます。

t検定の場合，このトレンドを考慮することができず平均値差しか見ないため，Phase AとPhase Bで傾きが同じ (バージョンBの効果がない) のに，効果があるように見えてしまいます。

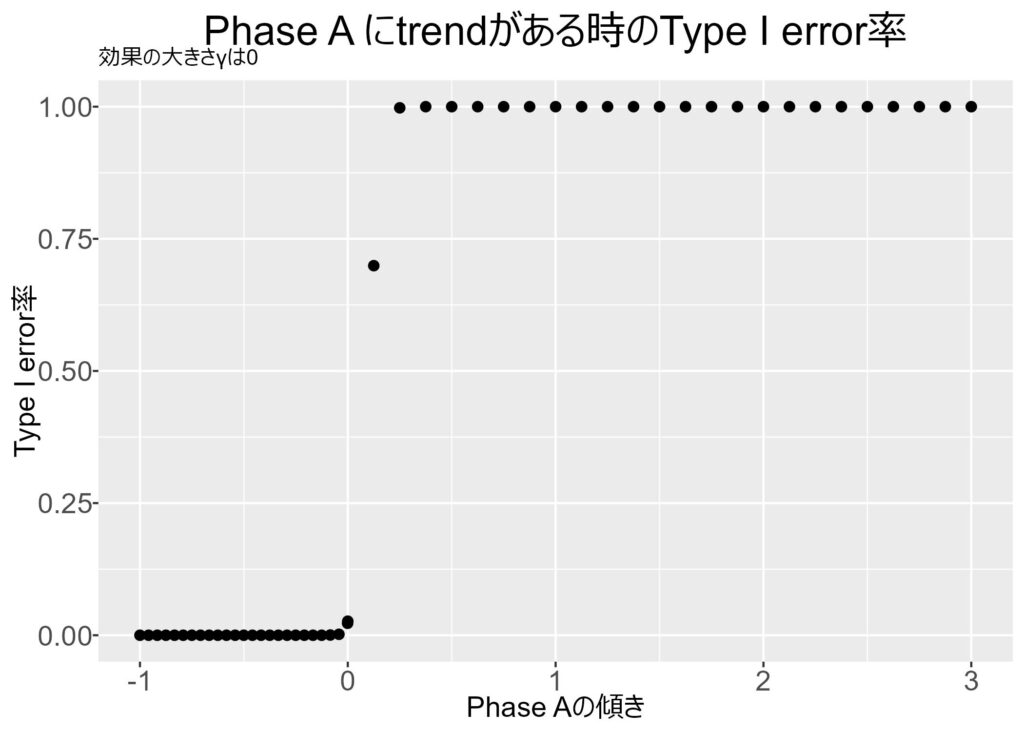
実際，シミュレーションをしてみると，以下の図のように「効果はないというのが真の状態」なのに，Phase Aの傾きが0以上の場合は有意差が見いだされてしまっています (Type I error率が上昇する)。

シミュレーションコード

シミュレーションコードは以下になります。既に関数として定義しているので，分量は少ないです。

mu_T <- 0 # ベースラインの平均
seqN <- 50 # 条件数
beta0_seq <- c(seq(-1, -0.001, length.out=seqN/2), seq(0, 3, length.out=seqN/2)) # phase Aのtrendの条件
res_plot <- numeric(length = seqN) # 格納用
for(i in 1:seqN) {
  res_plot[i] <- cond_sim(mu = mu_T,beta0 = beta0_seq[i],beta1 = 0,gamma = 0,phi = 0,sigma = 1,n0 = 10,n1 = 10, Iter = 5000)
}

自己相関が高い場合にType I error率が上がる

自己相関が正の方向に大きいということは，値が固まりやすいため，平均値差が見いだされやすくなってしまいます。そのため，効果がない時にも，効果があると判断されやすくなりType I error率が上がります。

以下の図は，自己相関とデータのsdを動かした時の，Type I error率の値です。最大で0.35ぐらいまでは上昇します。
特に自己相関が高い値だとType I error率が0.05に収まっていないのが分かります。
ちなみに，見えづらいですが，データのsdが大きくなると，ややType I error率が上がる傾向にあります (ただし自己相関は中程度の正の値)。

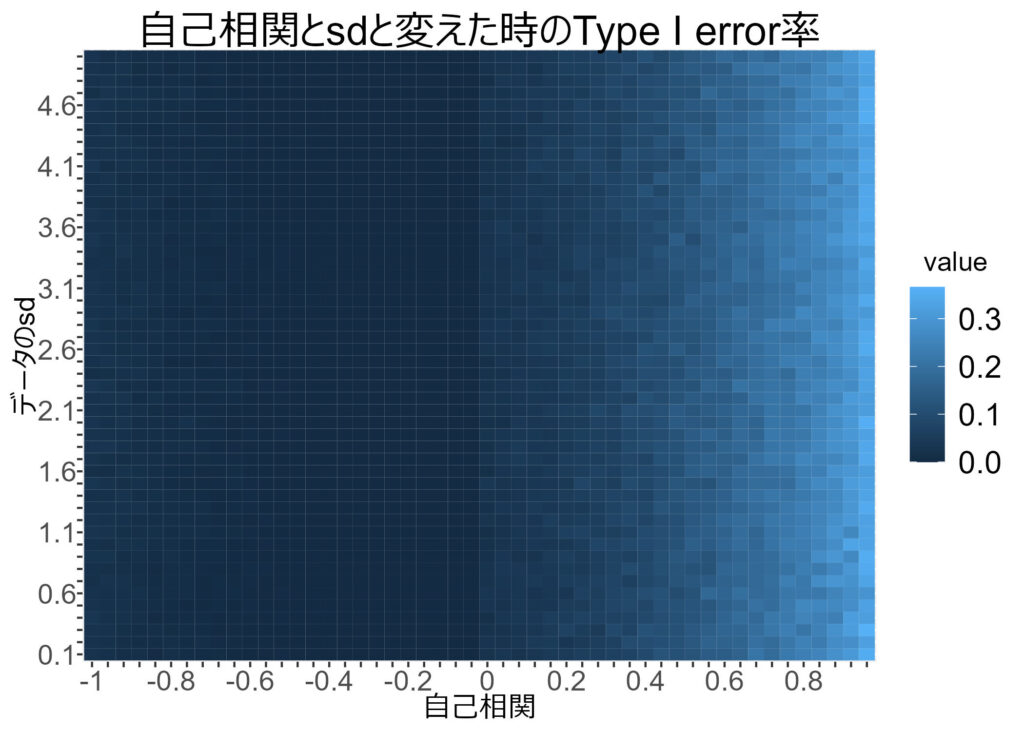
なお，自己相関が負の場合，0.05以下の値となっているので良さそうに見えますが，逆に値が低すぎるため検出力が低いことが示唆されます。実際，シミュレーションをしてみると，自己相関が負の場合，効果があるのが真の状態でも効果があると判断されにくくなります (記事の最後のシミュレーションを参照)。

シミュレーションコード

phi_cond <- c(-0.5, -0.2, 0, 0.2, 0.5, 0.6, 0.7) # 自己相関の条件
N12_cond <- c(5, 10, seq(20, 99, by=10), seq(100, 300, by=50)) # データ数条件
res_plot <- matrix(NA, nrow = length(phi_cond), ncol = length(N12_cond)) # 格納用
for(i in 1:length(phi_cond)) {
  for(j in 1:length(N12_cond)) {
    res_plot[i, j] <- cond_sim(mu = mu_T,beta0 = 0,beta1 = 0,gamma = 0,phi = phi_cond[i],sigma = 1,
                               n0 = N12_cond[j],n1 = N12_cond[j],Iter = 2000)
  }
  print(i)
}

逆方向のトレンドがある場合は，検出力が下がる

Web広告の効果を調べたという状況を考えます。ただし，企業の業績は調子が悪く，売上は下降傾向にある (傾きが負) としましょう。このような状況でWeb広告を打ってみると，売上の傾きが0あるいは上昇傾向に転じたとします。 (かなり極端な例です)

このような場合，明らかに効果はありますし，傾きの方向を変えるほどの効果はかなり大きく感じられます。しかし，単純なt検定やカイ二乗検定では平均値差しかみていないため，効果はないと判断されやすくなります。

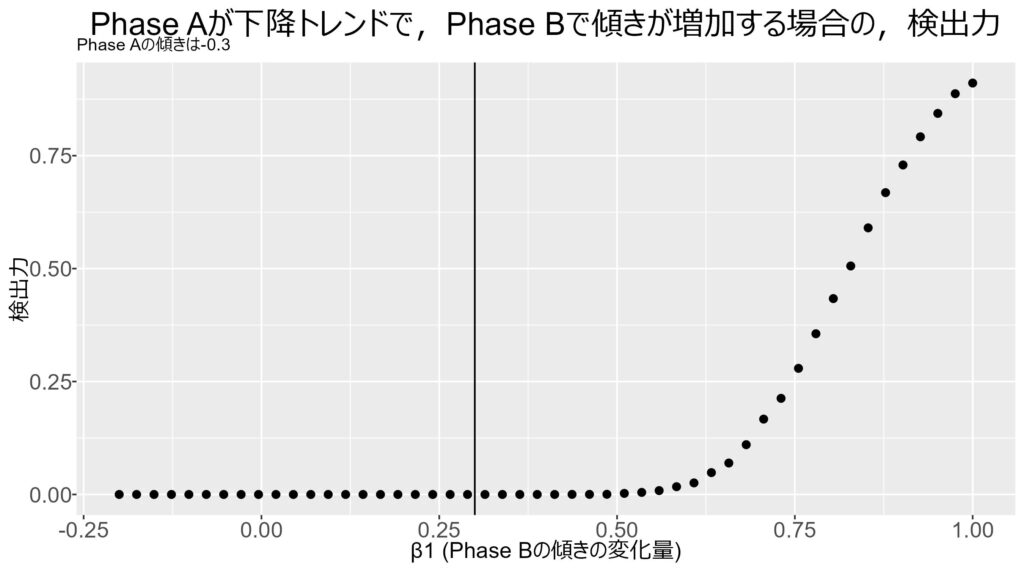
この図を見ると分かるように，Phase Aの傾きβ0が-0.3だった場合，Phase Bの傾きβ1は2倍の0.6ほどの傾きがないと検出力は高くなりません。

このような場合でも，きちんと統計モデルを記述し，Phase AとPhase Bの傾きを考慮するか，別々に推定してあげる必要があります。

シミュレーションコード

beta0 <- -0.3 # phase A の傾き
seqN_beta1 <- 50 # データ数
beta1_seq <- seq(-0.2, 1, length.out = seqN_beta1) # phase B の傾きの変化量 (式を参照)
res_plot <- numeric(length = seqN_beta1) # 格納用
for(i in 1:seqN_beta1) {
  res_plot[i] <- cond_sim(mu = mu_T,beta0 = beta0,beta1 = beta1_seq[i],gamma = 0,
                          phi = 0,sigma = 1,n0 = 10,n1 = 10,Iter = 5000)
}

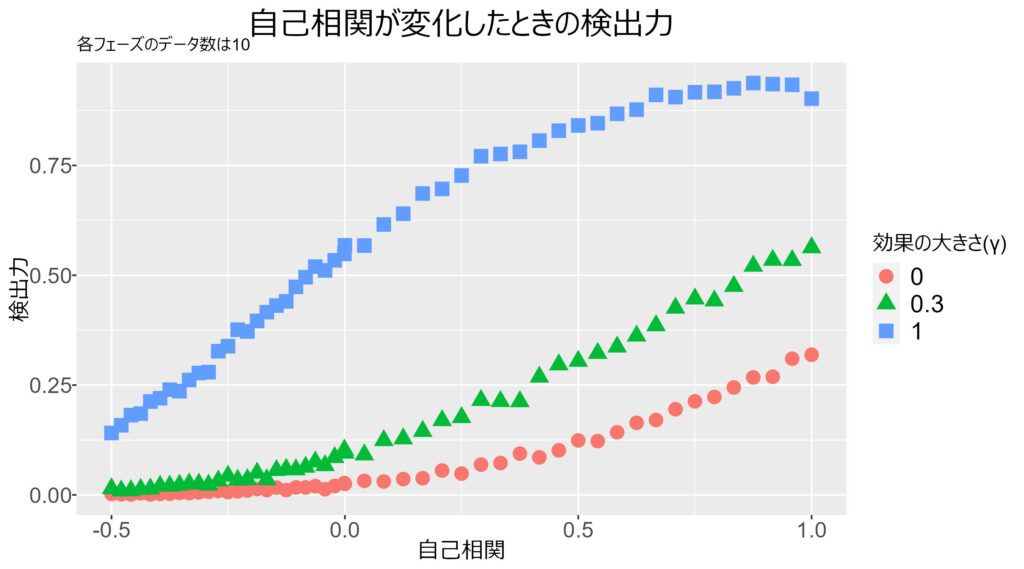
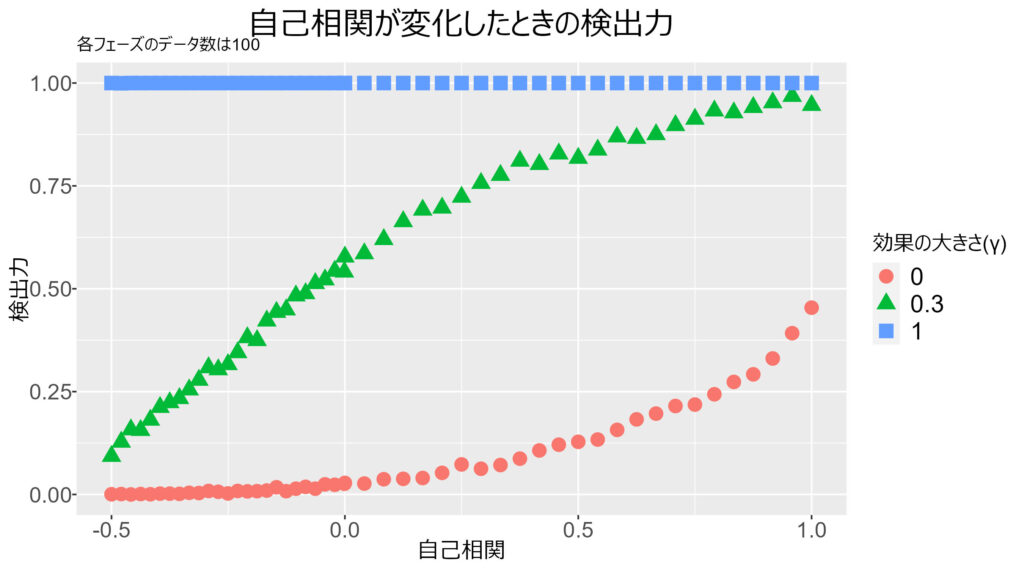
自己相関が負の場合に検出力が低い

以下の図を見てください。

自己相関 (x軸) が負の場合，いくら効果の大きさ (γ) が大きくても，検出力は低いことが分かります。

まとめ

以上4つのシミュレーションで示してきたように，単純なt検定やカイ二乗検定をABテスト (逐次テスト) に適用すると，Type I error率が増大したり，検出力が低くなってしまいます。

そのため，しっかりと時系列モデリングを行い，Phase A, Bの傾きや水準，自己相関を推定したうえで，効果の大きさを図っていく必要があります。

ニーズと機会があれば，ABテスト (逐次テスト) におけるモデリングの話題も執筆しようと思います。質問等があれば，コメントお待ちしております。